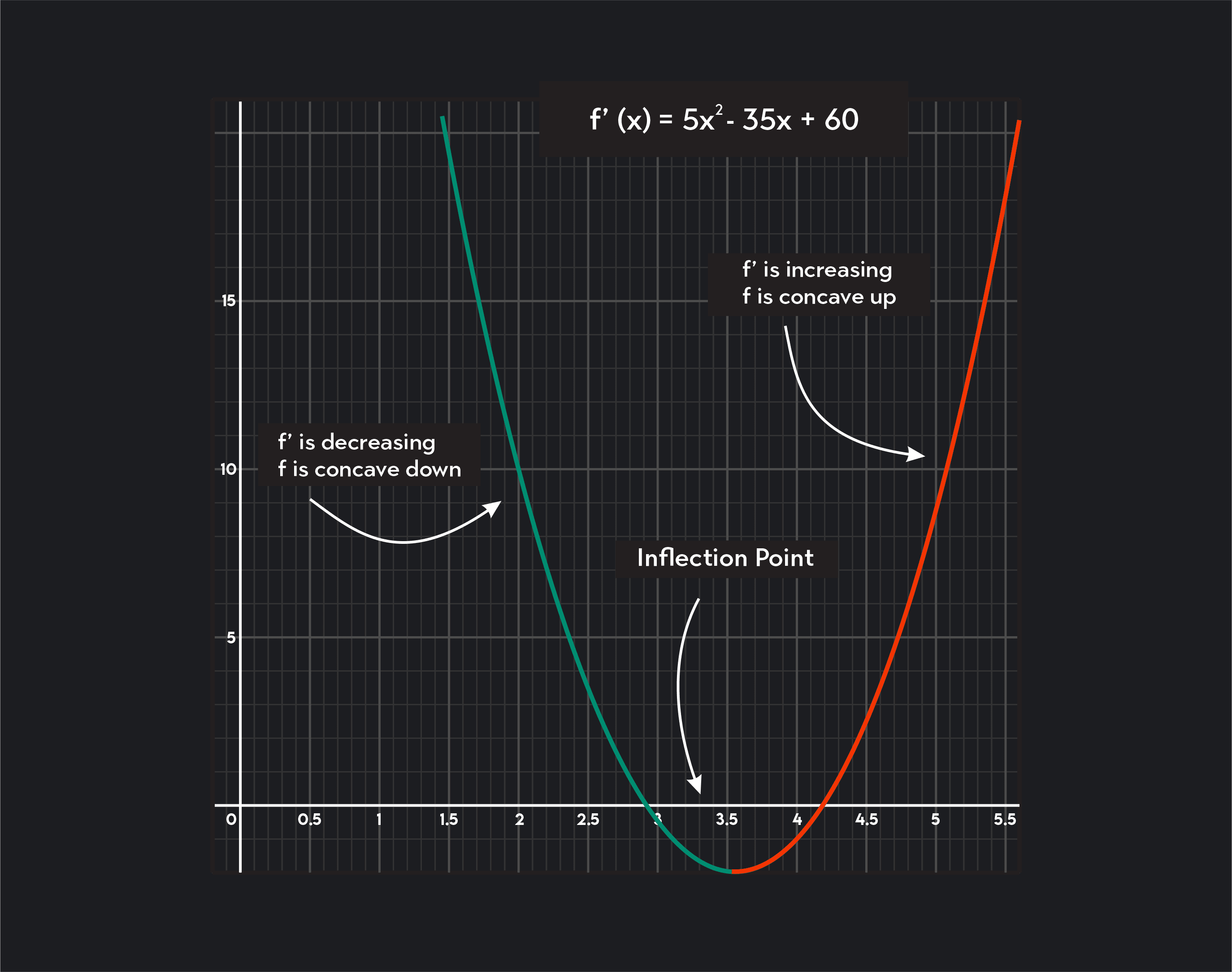
Point Of Inflection Non Continuous Function . the third kind of stationary point is a point of inflection. let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. And the inflection point is where it goes from concave upward to concave downward (or. when the second derivative is negative, the function is concave downward. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. review your knowledge of inflection points and how we use differential calculus to find them. The point x _ {0} is called a. Since it is a stationary point, dy = 0. Since it is also a point of inflection d2y.
from articles.outlier.org
when the second derivative is negative, the function is concave downward. Since it is a stationary point, dy = 0. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. The point x _ {0} is called a. And the inflection point is where it goes from concave upward to concave downward (or. review your knowledge of inflection points and how we use differential calculus to find them. Since it is also a point of inflection d2y. the third kind of stationary point is a point of inflection. the point where the function is neither concave nor convex is known as inflection point or the point of inflection.
Inflection Point Definition and How to Find It in 5 Steps Outlier
Point Of Inflection Non Continuous Function review your knowledge of inflection points and how we use differential calculus to find them. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. And the inflection point is where it goes from concave upward to concave downward (or. let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. the third kind of stationary point is a point of inflection. Since it is a stationary point, dy = 0. Since it is also a point of inflection d2y. when the second derivative is negative, the function is concave downward. The point x _ {0} is called a. review your knowledge of inflection points and how we use differential calculus to find them. the point where the function is neither concave nor convex is known as inflection point or the point of inflection.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Non Continuous Function The point x _ {0} is called a. when the second derivative is negative, the function is concave downward. Since it is a stationary point, dy = 0. review your knowledge of inflection points and how we use differential calculus to find them. the third kind of stationary point is a point of inflection. the point. Point Of Inflection Non Continuous Function.
From www.nagwa.com
Question Video Finding the Inflection Point of a Function Using the Point Of Inflection Non Continuous Function the third kind of stationary point is a point of inflection. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. Since it is a stationary point, dy = 0. Since it is also a point of inflection d2y. when the second derivative is negative, the function. Point Of Inflection Non Continuous Function.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. when the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave upward to concave downward (or. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. the point. Point Of Inflection Non Continuous Function.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. when the second derivative is negative, the function is concave downward. review your knowledge of inflection points and how we use differential calculus to find them. let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at. Point Of Inflection Non Continuous Function.
From mungfali.com
How To Find Inflection Points Of A Function Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. when the second derivative is negative, the function is concave downward. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. the point where the function is neither concave nor convex is known as inflection point or the. Point Of Inflection Non Continuous Function.
From www.youtube.com
Finding Points of Inflection and Intervals of Concavity Calculus Point Of Inflection Non Continuous Function The point x _ {0} is called a. when the second derivative is negative, the function is concave downward. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. an inflection point is a point on a curve at which the sign of the curvature (i.e., the. Point Of Inflection Non Continuous Function.
From mathemerize.com
What is the Point of Inflection ? Mathemerize Point Of Inflection Non Continuous Function And the inflection point is where it goes from concave upward to concave downward (or. let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. when the second derivative is negative, the function is concave downward. review your knowledge of inflection points and. Point Of Inflection Non Continuous Function.
From www.radfordmathematics.com
Point of Inflection Calculus Point Of Inflection Non Continuous Function let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. when the second derivative is negative, the function is concave downward. Since it. Point Of Inflection Non Continuous Function.
From www.geogebra.org
NonStationary Points of Inflection GeoGebra Point Of Inflection Non Continuous Function the third kind of stationary point is a point of inflection. The point x _ {0} is called a. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. an inflection point is a point on a curve at which the sign of the curvature (i.e., the. Point Of Inflection Non Continuous Function.
From articles.outlier.org
Inflection Point Definition and How to Find It in 5 Steps Outlier Point Of Inflection Non Continuous Function the third kind of stationary point is a point of inflection. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. Since it is a stationary point, dy = 0. an inflection point is a point on a curve at which the sign of the curvature (i.e.,. Point Of Inflection Non Continuous Function.
From studywell.com
Convex And Concave Functions And Inflection Points Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. The point x _ {0} is called a. the point where the function is neither concave nor convex is known as inflection point or the. Point Of Inflection Non Continuous Function.
From study.com
Finding Inflection Points and Concavity Overview & Examples Lesson Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. Since it is a stationary point, dy = 0. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. The point x _ {0} is called a. the third kind of stationary point is a point of inflection. And. Point Of Inflection Non Continuous Function.
From dxolgwuqu.blob.core.windows.net
Point Of Inflection And Contraflexure at Katherine Cruz blog Point Of Inflection Non Continuous Function The point x _ {0} is called a. Since it is also a point of inflection d2y. the third kind of stationary point is a point of inflection. Since it is a stationary point, dy = 0. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. And. Point Of Inflection Non Continuous Function.
From www.savemyexams.com
Points of Inflection AQA A Level Maths Pure Revision Notes 2018 Point Of Inflection Non Continuous Function The point x _ {0} is called a. when the second derivative is negative, the function is concave downward. And the inflection point is where it goes from concave upward to concave downward (or. the third kind of stationary point is a point of inflection. let a function f be defined in a certain neighbourhood around a. Point Of Inflection Non Continuous Function.
From www.youtube.com
Integral of a Non Continuous Function YouTube Point Of Inflection Non Continuous Function when the second derivative is negative, the function is concave downward. the third kind of stationary point is a point of inflection. an inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. Since it is also a point of inflection d2y. Since it is a stationary point,. Point Of Inflection Non Continuous Function.
From www.savemyexams.com
Points of Inflection AQA A Level Maths Pure Revision Notes 2018 Point Of Inflection Non Continuous Function let a function f be defined in a certain neighbourhood around a point x _ {0} and let it be continuous at that point. review your knowledge of inflection points and how we use differential calculus to find them. Since it is also a point of inflection d2y. The point x _ {0} is called a. Since it. Point Of Inflection Non Continuous Function.
From www.linstitute.net
IB DP Maths AI HL复习笔记5.2.6 Concavity & Points of Inflection翰林国际教育 Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. The point x _ {0} is called a. when the second derivative is negative, the function is concave downward. the third kind of stationary point is a point. Point Of Inflection Non Continuous Function.
From exolzpkik.blob.core.windows.net
Points Of Inflection Of A Function at Freddie Braun blog Point Of Inflection Non Continuous Function Since it is also a point of inflection d2y. the third kind of stationary point is a point of inflection. when the second derivative is negative, the function is concave downward. the point where the function is neither concave nor convex is known as inflection point or the point of inflection. And the inflection point is where. Point Of Inflection Non Continuous Function.